Last Modified: 30 September 2012
The Design and Construction of Low Frequency Chokes and Single-Ended Output Transformers
The Low Frequency Choke is used in the power supply to filter out hum from the current supply. In power supply smoothing, DC is flowing.
The effect of DC in the winding is to decrease the incremental permeability of the core material – in practice a laminated core is used as in the transformer – so that the iron saturates more rapidly and the inductance of the choke is lowered. This induction loss can only be partially countered by arranging to have a small air gap between the sets of laminations in the assembled core.

Figure 04
For chokes carrying AC alone, therefore, the laminations are interleaved as are those in a transformer, but for a choke carrying DC and AC the laminations are assembled with the two sets of stampings one on each side – that is all the E's on one side and all the I's opposite (or all T's together opposite all U's, whichever type of stamping is used), and it will be seen that in the core assembled in this manner there will be three air gaps, one at the end of each limb (Figure 04 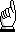 ). So far as the magnetic circuit is concerned, even a tightly clamped butt joint acts as a small air gap, and for correspondingly larger air gaps a piece of thin paper may be inserted between the end of each limb and the opposite laminations. The calculation of the correct air gap for any single case is rather involved, however, and it is recommended that for mixed AC and DC operation the gap should be decided upon by experiment. As a rough guide it may be said that the close butt joint will do for currents of 5 or even 10 milliamps, but for higher currents the gap must be widened by inserting a 0.0005 inch sheet of paper or more. (Originally the 'air gap' is acheived with waxed paper.)
). So far as the magnetic circuit is concerned, even a tightly clamped butt joint acts as a small air gap, and for correspondingly larger air gaps a piece of thin paper may be inserted between the end of each limb and the opposite laminations. The calculation of the correct air gap for any single case is rather involved, however, and it is recommended that for mixed AC and DC operation the gap should be decided upon by experiment. As a rough guide it may be said that the close butt joint will do for currents of 5 or even 10 milliamps, but for higher currents the gap must be widened by inserting a 0.0005 inch sheet of paper or more. (Originally the 'air gap' is acheived with waxed paper.)
Chokes for Mixed AC and DC Currents
Where the choke is to carry DC as well as AC it will scarcely be possible to wind such a high inductance as e.g. 100 H (should it be needed) on a small core unless the DC component is practically negligible. In the first place the wire would need to be of a heavier gauge to carry the current as well as to reduce the DC resistance to as low a figure as possible.
For example, it may be necessary to use a choke as the anode load for a valve for the reason that a suitable resistance load reduces the anode voltage to too low a figure. The choke will still present a high impedance to the AC signal but the DC resistance must be low or otherwise the whole purpose of the choke will be defeated. This means a thicker gauge of wire and therefore a larger core, for the number of turns must still be high to maintain the inductance and therefore the impedance to the signal.
The simplest way out of the difficulty is to measure the winding space of the core to be used and choose a gauge of wire which when wound to fill the space will give a DC resistance suitable for the permitted voltage drop. This may be done by taking the length of an average turn on the winding limb, multiplying the number of turns given by the wire table by this length to find the whole length of wire in the winding, and then to check the resistance of this length in the wire tables.
The length of the average turn is, of course, the average of the length of the first and last turns on the winding and may be measured on the cheek of the core supposing the average turn to be geometrically situated at half the winding depth.
Smoothing chokes may be wound in this way. Choose a suitable core with a cross sectional area of at least 1 square inch and a window space of at least 2 square inches and decide from the wire tables the gauge of wire which will carry the maximum current safely, using a current density of 1,500 or 2,000 amperes per square inch. Enamelled copper wire (ecw) is suitable for the winding and again the layers should not need to be interleaved, the space which would be used by the paper being of greater value if filled with wire.
The gap can be adjusted experimentally by allowing the choke to supply filtered DC to a sensitive receiver or amplifier. The core clamping bolts are loosened just sufficiently to allow the sets of laminations to be moved and the space between them is gradually opened until the hum in the loudspeaker, with no signals and the gain control right out, is at a maximum. The gap can then be set with a paper or very thin fibre packing and the core reclamped.
Chokes Carrying Direct Current
Inductance
Chokes of this type are generally required for one of two purposes: (1) Smoothing, and (2) Coupling. In either case, the inductance necessary is based on the impedance which it will have at a certain frequency. For smoothing, this frequency is that of the ripple to be eliminated in smoothing, and for coupling chokes it is the lowest frequency required to be reproduced.
The reactance of an inductance is given by the formula: -
XL = 2 Π f L,
where Π is 3.14, f is the frequency and L the inductance in Henries.
For a smoothing circuit, the condenser reactance must also be known, and this is given by the formula: -
XC = 1,000,000/2 Π f C
where C is the capacity in microfarads.
If a smoothing circuit is required to reduce the ripple voltage to 1/40th of that across the reservoir condenser, then the required ratio of reactance of smoothing choke and condenser will be given by
Xc / XL = 1 / 40
Assuming an 8 μF electrolytic condenser is to be used (as was in the old days, much larger values can be had now), then its reactance to a ripple voltage of 100 Hz (the predominant frequency from a 50 Hz full wave rectifier) will be
1,000,000 / (2 x 3.14 x 100 x 8) = 200 ohms approx.
Therefore, the reactance of the choke must be 40 x 200 or 8,000 ohms. From the formula, 8,000 = 2 Π 100 L, therefore:
L = 8,000 / (2 x 3.14 x 100) nearly 13 Henries.
In the same way, the inductance can be calculated for any given degree of smoothing.
These values of inductance must not be regarded as obtainable to great accuracy, as the actual value for any given applied AC voltage is dependent on the DC current flowing at the time, and on the amplitude of the AC voltage. Because of this fact, it is always good to allow a little in hand, so that performance will not vary too much if operation should change, due to changes in mains voltage. It would be well to design the chokes in the above examples to have inductances of, say, 15 and 40 Henries respectively.
Current and Volt Drop
The direct current to be carried by the choke will be fixed by other considerations. In the case of the smoothing choke, by the total current to be taken by the set, and in the case of the coupling choke by the anode current of the valve. As well as being required to give the required inductance at this current, there will usually be an additional requirement that the choke shall not drop more than a certain voltage DC across it, due to its resistance.
We now have three factors, which roughly determine how large the choke must be physically. These three factors and the size do not have some simple relation, such as that the size of the choke in, say, cubic inches, is equal to the inductance x current x volt drop. For this reason, Table 1 gives a quick means of finding a suitable design.
| Table 1. Values of Current and Inductance for Choke to Dimensions of Figure 04 (approximately) | ||||
| Current milliamps |
Inductance Henries |
Resistance Ohms |
Volts dropped |
Turns |
| 10 | 30
50 70 100 150 200 |
100
200 350 550 1000 1600 |
1.00
2.00 3.50 5.50 10.00 16.00 |
2200
3200 4100 5300 7300 9000 |
| 15 | 10
15 20 30 50 70 |
30
50 75 140 300 500 |
0.45
0.75 1.10 2.10 4.50 7.50 |
1200
1600 2000 2700 3900 5000 |
| 20 | 10 15 20 30 50 70 |
35 65 100 180 400 650 |
0.70 1.30 2.00 3.60 8.00 13.00 |
1400 1800 2200 3000 4500 6000 |
| 30 | 10 15 20 30 50 70 |
55 100 150 270 600 1000 |
1.70 3.00 4.50 8.10 18.00 30.00 |
1700 2200 2800 3700 5700 7300 |
| 50 | 10 15 20 30 50 70 |
90 160 250 450 1000 1600 |
4.50 8.00 12.50 23.00 50.00 80.00 |
2100 2900 3600 4800 6500 9000 |
| 70 | 5 7 10 15 20 30 |
45 75 120 230 350 650 |
3.00 5.00 8.50 16.00 24.00 45.00 |
1500 2000 2500 3400 4100 6000 |
| x÷ 10 | x÷ 10 | x÷ 100 | x÷ 3.2 | |
| x÷ 10 | x÷ 32 | x÷ 32 | x÷ 5.6 | |
For most practical purposes, it may be mentioned that again the Transformer Kits could be pressed into service to create LF chokes of 5 to 10 Henries or more. The nature of each kit allows access to the individual laminations which therefore can readily be assembled in all E's on one side and I's on the other to form an 'air gapped' core.

Figure 06
Using The Choke
In a power supply the LF choke is used as shown in Figure 06 (right). Where C1 is the reservoir, C2 forms a LC low-pass filter with L1. Because of the shape descibed by these three components in a circuit diagram, the configuration is colloquially known as a 'pi' filter, i.e. a three sided shape like the Greek letter Π (as are cascaded resistor attenuator networks called 'pi' attenuators).
In some circumstances, either to save space or costs, C1 may be omitted entirely; the remainder still providing adequate filtering and with C2 functioning as the reservoir, especially if the value of C2 is large. It also helps avoid over-emission stresses in the valve due to working into a large value capacitive load.
Output Transformer For A Single Valve (single-ended output)
Turns and Impedance Ratio
Because of its close similarities with the LF choke carrying DC, it is relevant to mention the single-ended or class A audio output transformer for a single power valve here. The purpose of this type of transformer is to match the impedance of a loudspeaker, or group of loudspeakers, to the optimum load of the valve. That is, the transformer has the effect of transforming the impedance of the speaker so that the impedance which it presents in the primary winding is equal to the optimum load of the output valve.
Moreover, since the transformer is driven by a single valve (known as single-ended mode or single-ended power amplifier), there is DC present in the primary winding so the core shares the need for an air gap with the smoothing choke; in this construction and in other respects the components are very similar.
A typical single-ended power amplifier of a few watts output and using one of these transformers is shown below.

Figure 28
It is well known that the impedance ratio of a transformer is equal to the square of the turns ratio, conversely, the turns ratio is equal to the impedance ratio squared. It is also worth mentioning that the turns and Voltage ratios are the same. Also, that the inductance and impedance ratios are the same (for example inductance ratio is what CAD programs such as LTspice use to specify the ratios of coupled windings).
Impedance/Turns Relationship
This depends on the DC current flowing in the primary, on the size and shape, and on the lowest frequency required. To make calculation easier, if the actual DC current flowing in the primary is referred to a theoretical 1,000 ohms winding, then the turns for such a winding can readily be found, and from that the turns in the actual windings determined. Using this reference, the current in this winding will bear a relationship to the maximum output power which will vary very little, although widely different types of valve may be used.
Table 2 gives a series of reference figures. For each value of current referred to 1,000 ohm winding, is given two figures for the turns in a 1,000 ohm winding: one for general use, giving a low frequency cut-off of 50 Hz, and the other for special use when a circuit is used for speech only, giving a low frequency cut-off of 200 Hz. For each value of current is given an approximate figure of maximum output. This may be found useful if some of the valve data is not obtainable (e.g., the optimum load). For each value of current and cut-off is given the approximate percentage loss due to winding resistance.
Choice of Size
The figures in Table 2 are for the same core dimensions as those approximately shown in Figure 04. In practice, for an output transformer it will be better from the constructional viewpoint if the stack is less than twice the A dimension, preferably equal to it. The chief factor in determining size is the amount of power that can be allowed as loss in the transformer. The appropriate loss factors for other sizes may be found from the figures given by multiplying or dividing by the Resistance Factor given in sections 2-5 of Table (below) 3 for the appropriate shape and size.
| Table 2. Impedance/Turns Relationship for Core of Size approximately shown in Figure 04 | |||||
| 50 Hz cut-off | 200 Hz cut-off | ||||
| DC | |||||
| referenced to 1000Ω |
Turns for 10000Ω |
Series loss |
Turns for 1000Ω |
Series loss |
Max. power |
| 50 70 100 150 200 |
900 1100 1300 1600 1900 |
7% 9% 13% 20% 28% |
310 380 450 550 650 |
1.0% 1.3% 2.0% 3.0% 4.0% |
800 mW 1.5 W 3.0 W 7.0 W 12.0 W |
Having chosen a suitable size, the number of turns for a 1,000 ohm winding can be found by use of the Turns Factor in the same table, applied to the value given in Table 2.
Example for music reproduction
Calculate the turns required to match a 15 ohm speaker to a valve having an optimum load of 4,500 ohms, and an anode current of 48 milliamps for general use on music and speech. It should be at least 90% efficient.
If 48 milliamps are flowing in a winding of impedance 4,500 ohms, then the equivalent in a 1,000 ohms winding will be:
48 x √(4,500/1,000) = 100 mA approx.
From this value in Table 2 it is seen that on the size shown in Figure 04 for a 50 Hz cut-off, 1,300 turns for 1,000 winding give a loss of 13%.
To have at least 90% efficiency, the loss must be at most 100 – 90 = 10%. This means that a size must be chosen with a dividing Resistance Factor of at least 1.3. The following sizes satisfy this, where the dimensions in inches are as follows: A, width of central limb of core; B, total width of core; C, total height of core; stack, thickness of laminations:
| Section No. | Dimensions | Stack |
Turns factor |
Resistance factor | ||
| A | B | C | ||||
| 2 3 4 5 |
1.000 1.125 0.875 1.000 |
3.5000 3.0000 3.4375 3.0000 |
2.500 2.250 2.500 2.500 |
1.000 0.750 0.625 1.000 |
X 1.2 X 1.4 X 2.0 X 1.2 |
÷ 1.4 ÷ 1.7 ÷ 1.4 ÷ 1.3 |
It will be noticed that there is little difference in size, and therefore there is not much to choose as to which is the best to use. Assume that a size similar to the one from Table 3 (above) is available, then the loss will be 13 ÷ 1.7 = 7.6% and the efficiency 100 – 7.6 = 92.4%. The turns for a 1,000 ohm winding will be 1.4 x 1,300 = 1,800 approx. Then the turns for a 4,500 ohm winding will be:
1,800 x √(4,500/1500) = 3,800.
The turns for the 15 ohm winding will be:
1,800 x √(15/1,000) = 220.
Thus the transformer will require a primary of 3,800 turns, and a secondary of 220 turns.
Example for speech only (Public Address) reproduction
The only details known about an output valve are that with 450 volts HT it should give about 12 watts output, taking an anode current of 120 milliamps. It is required to match a horn type speaker for use on speech only, with an efficiency of about 90%. The speech coil impedance is 4.5 ohms.
From Table 2 it is seen that 12 watts corresponds to a current referred to a 1,000 ohms winding of 200 mA. The actual current is 120 mA, so the optimum load must be:
1,000 x 2002/1202 = 2,800 ohms.
Also the loss for a 200 Hz cut-off type on this size is only 4%. As the efficiency is only required to be 90%, the loss can be up to 10%. This means a smaller size can be used, which may facilitate fitting the transformer into the horn housing. Thus the resistance can be multiplied by 2.5 (but not more). It will be seen that a 3/4 inch stack of the same lamination will give a resistance factor of x 2.3. An alternative may be found using a 3/4 inch stack of a similar size. In either case the turns factor is x 1.7, so the calculation of turns in this case will be the same whichever is chosen.
From Table 2 the turns for a 1,000 winding are 650. So for this size the turns will be 1.7 x 650 = 1,100. The turns for a 2,800 ohms winding will be:
1,100 x √(2,800/1,000) = 1,850.
The turns for the 4.5 ohm winding will be:
1,850 x √(4.5/2,800) = 74.
The ratio in this case is 1,850/74 = 25/1.
Special Precaution for 200 Hz Cut-off
When an amplifier is to be used under conditions required to operate a loudspeaker having a 200 Hz cut-off (i.e., a PA horn type), there are two precautions necessary: (1) To see that no signal or any considerable amplitude reaches the speaker. This is to prevent damage to the speaker itself, or the introduction of distortion by it due to receiving frequencies which it is not designed to handle. (2) To see that no signal of a lower frequency which may be present in the amplifier causes distortion to frequencies which do reach the loudspeaker.
This second requirement means either that the output of the amplifier must be correctly matched at these frequencies, although arrangement is made so that they do not reach the speaker, or that arrangement must be made to ensure that these frequencies do not reach the output stage of the amplifier.
It is therefore necessary, when using a 200 Hz cut-off type, to take steps to ensure that there is a similar cut-off in the amplifier, somewhere before the output stage. This should take the form of a coupling condenser whose impedance at 200 Hz is equal to that of the grid leak following it.
Air Gap Determination
With each of these types of component, either LF choke or single-ended output transformer, there is DC flowing in one of the windings which has a tendency to saturate the iron core. For this reason an air gap is employed, instead of laminating the transformers in the manner required for push-pull output transformer types.
For any given case, too small an air gap will result in the magnetic flux due to the DC component producing saturation, while too large a gap will cause loss of inductance because of the magnetizing current necessary to drive the AC component of flux across the air gap.
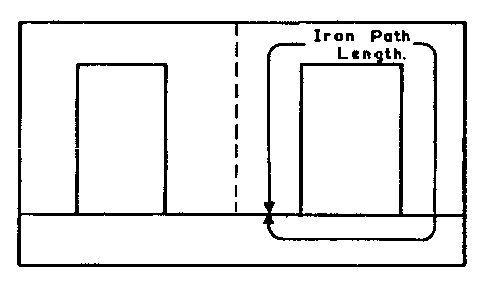
Figure 05
The chief factor which determines the best air gap for any given example is the total effective DC magnetizing force, which may be expressed in ampere-turns – that is to say, the current in amperes multiplied by the turns in the winding. The type of transformer iron used, and the length of iron path (see Figure 05), both have a slight effect upon the best gap, and on the resulting inductance. As the effect of different iron is so slight, the use of more expensive irons is not considered worth the extra cost in general, so the only iron considered here is ordinary grade transformer iron (usual lamination thickness about 0.016").
If equipment is available to test the component for inductance under the operating value of DC current then the ideal practicable thickness of material inserted into the air gap may be determined. Deviations will generally be due to practical variations on account of difficulties in clamping up. You could start with a close gap (metal to metal) then experiment with the gap to acheive the lowest desired inductance.
If such equipment is not available, then care should be taken to produce as near to the optimum gap as is possible, making slight allowances if the edges of the laminations should have been slightly burred in stamping.
