Last Modified: 30 September 2012

Valve Theory + Transformers and Chokes


[Previous] [Next] [Contents]

Basic Valve Amplifier Circuits

Similar to the transistor, the triode may be used in three different configurations:

The Common Cathode is the most popular connection and this will be dealt with in some detail.

The vacuum triode has three internal elements: cathode, control grid, and anode. Multiple grid valves, such as pentodes or hexodes, have the same basic elements to which are added extra grids for special functions.

The basic circuits represent the three possible choices of common electrode, to form a four-terminal or two-port device. The grounded- or common-cathode circuit (Figure 19(a)) was the earliest form and remains the most used. (The cathode-follower [Figure 24] is of use for coupling a high impedance to a lower impedance level, serving the same function as the emitter-follower transistor circuit.) The grounded-grid circuit provides step-up impedance characteristics, paralleling the function of the common-base transistor circuit.


The Grounded-Cathode Amplifier Circuit
Usual circuit connections for both triode and pentode in the grounded-cathode circuit are shown in Figure 19 *: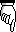



Figure 19
Figure 19

The functions of the cathode resistor Rk, and the screen-dropping resistor Rs, for the pentode will be discussed in the next section; they may be considered shunted out of the equivalent signal-frequency circuit by their bypass capacitors.

Since Eo = –RLIP, the output voltage can be written as:

Eo = –μ RLEg
Eo = –rp + RL

Since the input current is assumed zero for the negative grid, current gain of the triode or pentode has no meaning. Voltage gain is defined as for the transistor, as the ratio of the output voltage rise to the input voltage rise. Then:

Av = Eo = Eo = –μ RL
Av = Eg = Es = rp + RL

= –gmRL
= 1 + RL/rp

The angle associated with the result is the phase shift of the amplifier; for a resistive load it is 180° in this circuit.\br
Figure 20(a) (graph 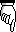*) shows the variation of gain vs. load for a triode of μ = 20. With resistive load, the DC voltage drop in large loads lowers Eb and raises rp, and the gain does not continue to rise for very large load resistors.


Figure 20
Figure 20

Since the current-source circuit is appropriate for pentodes, its use allows the pentode gain to be written as:

Eo = –gmRLEg

Av = Eo/Eg = Eo/Es = –gmRL

The gain is proportional to gm for both triode and pentode, and gm becomes an important performance criterion.


The DC Bias Sources
In practice it is most convenient to provide the grid-bias DC voltage for the valve by insertion of a resistor, Rk, in the cathode lead (as opposed to a separate grid-bias battery cell). The polarity of the voltage developed across this resistor is negative to the grid, so as to place the operating point in the linear negative portion of the transfer characteristic, see also Figure 20(b) *.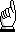

When presented with a input signal, an AC signal voltage is also developed across this resistor by the valve, and the effective gain is reduced because this AC voltage subtracts from the input signal voltage. This is a form of negative feedback. The reduction of gain can be prevented if Rk is paralleled by a capacitor, Ck, of small reactance with respect to Rk. Then the AC voltage across the Rk, Ck combination is negligible, and the combination can be dropped from the AC equivalent circuit.

The DC and AC components may be assumed to divide as in Figure 20(b) 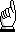*, and so the value of Rk can be determined from the relations:

Ecc = RkIb, Rk = Ecc / Ib

For pentodes the cathode current will also include the screen current, so that:

Rk = Ecc / (Ib + Ic2)

The capacitance Ck must be chosen as having a small reactance with respect to Rk at the lowest signal frequency; this requirement is usually met if Xc < Rk/10. Capacitor values for audio frequencies will range from 1 to l00 μ F.

The value of the screen dropping resistor for the pentode of Figure 19(b) (above 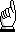*) can be found through use of the difference between Ebb and the desired screen potential, and the screen current; that is:

Rs = (Ebb – Ec2) / Ic2

Capacitor Cs must offer a small reactance with respect to the screen-cathode path within the valve, and this usually requires a reactance of less than a few hundred ohms at the lowest signal frequency.


Figure 21
Figure 21

The Input Circuit Of The Grounded-Cathode Amplifier
With reference to Figure 21 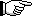*, the triode valve has internal electrode capacitances: Cgk between grid and cathode; Cgp between grid and anode; and Cpk between anode and cathode. These capacitances are of the order of 1 to 5 pF each. It might appear that the input admittance of the triode with negative grid would be wholly due to these capacitances; however, the active nature of the circuit alters the situation and the input appears as a resistance shunted by a capacitance as in Figure 22. This apparent input capacitance may exceed the actual geometric capacitance because of the additional effect of Cgp, and this phenomenon is known as the Miller effect.

The Miller Effect has been exploited for making ramped waveform generators; the valve is fed with a square-wave and extra capacitance is added between anode and grid to augment Cgp.

Figure 22
Figure 22

In summary, omitting overly complex mathematics at this point, the input admittance for the triode in the grounded-grid circuit is composed of resistance and capacitance as:

Rin = – 1 / (gm Ω Cgp(±X') (9-27)

Cin = Cgk + Cgp(1 + gmR') (9-28)




Referring to Figures 21 and 22, three cases arise from all these effects:

1. The load reactance may be capacitive, X' is then negative and Rin is a positive resistance which decreases with frequency. The input capacitance is Cin.

2. The load may be resistive and Rin is infinite. The value of Cin will be greater than Cgk and may be quite large for some triodes. Because of its small Cgp, the pentode's input capacitance will approximate Cgk.

3. The load reactance may be inductive and X' is positive, making Rin negative. The current Igp (grid to anode) then feeds power back to the input circuit from the anode circuit.

Whenever the power fed back is greater than the input circuit losses, the net circuit resistance is zero or negative, and the valve becomes an oscillator. It is also found that Cin becomes large for triodes at radio frequencies. The pentode has a very small Cgp by design, and is capable of satisfactory amplification at frequencies of several hundred megahertz in the grounded-cathode circuit.


Figure 23
Figure 23

The Grounded-Grid Amplifier
With the grid as the common element, the circuit of Figure 23 is known as a grounded-grid amplifier. The grounding of the grid provides shielding between input and output circuits. At radio frequencies this shielding reduces energy transfer between output and input and permits the use of triodes with resonant load circuits, without threat of capacitive feedback and oscillation, and triodes are so used for stable power gain in transmitters. Triodes also produce lower internal noise than do pentodes, and so the circuit is also useful as an input amplifier for radio receivers handling very weak input signals, practically at the inherent valve noise level, see also Composite Valve Amplifiers.
Equations for the two meshes are:

μ Eg – Es = Ip(rp + Rs + RL) (9-29)

Eg + Es = – IpRs (9-30)

The load rise from grid to anode is Eo = – IpRL, and since Es is given as a negative rise above common terminal, the gain can be written as:

Ao = (Eo/Es) = [(μ + 1) RL] / [rp + (μ + 1) Rs + RL] (9-31)

The output of the amplifier is in phase with the input for resistive load. Since E, is in series with the transfer generator, the input voltage adds to that of the generator, and the valve has an apparent amplification factor of μ + 1.

From Eq. 9-31 the effective output impedance can be found as:

Ro = rp + (μ + 1)Rs (9-32)

The input impedance at terminals a, a is:

Ri = (Eg/Ip) = (rp + RL)/(μ + 1) (9-33)

The input impedance appears as the resistance of the output circuit divided by μ + 1. For a valve of μ = 20, rp = 7700 ohms, and with a 50,000-ohm load, the input resistance is 2750 ohms.

Since there is power input to the stage, the power gain is of importance, as:

P.G. = (E2o/RL) / [E2o(μ + 1) / (rp + RL)] (9-34)

from terminals a, a to the output load.

The circuit is of use in transforming from a source of low impedance, such as an antenna, to a load of high impedance, in a fashion similar to the common-base transistor circuit.


The Cathode Follower
An amplifier with the anode as the common terminal is called a cathode follower. The name is logical because the cathode potential varies with and is almost equal to the input voltage. The circuit and its equivalent are shown in Figure 24. In (b) 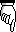*, the bias resistances are replaced by their parallel equivalent Rg.

Neglecting the valve capacitances, the mesh equations are:

Eg = Es – IpRk

μ Eg = 1p(rp + Rk)


Figure 24
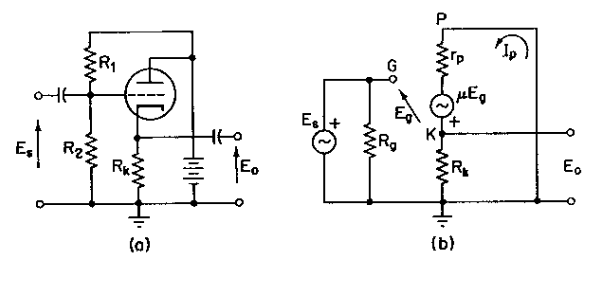
Figure 24

The voltage amplification can be found as:

Av = gmRk/1 + gmRk + (Rk/rp) = μ Rk/rp + (μ + 1)Rk = 1/1 + (1/gmRk) + (1/μ ) (9-35)

The gain is always less than but near unity, especially as gmRk increases. When a pentode is used, the screen bypass must connect to the cathode, since the screen must be held at cathode AC potential.

With a current I1 into the upper Eo terminal of Figure 24(b):

Eo = RkI1 + RkIp = – Eg (9-36)

μ Eg = RkI1 + (rp + Rk)Ip (9-37)

Solving for Ip and inserting the result in Eq. 9-36 givesthe output resistance as:

Ro = Eo/I1 = [rpRk/(μ + 1)] / [Rk + rp/(μ + 1)] (9-38)

The relation is that of two resistors in parallel, namely, Rk and the effective internal resistance of the valve, rp/(μ + 1) @ l/gm.

Since the gain is near but less than unity, the input capacitance is largely due to Cgp, and considerably less than that of the same valve in the grounded-cathode circuit.

The circuit is used as an impedance-matching device, to couple a high impedance source to a lower impedance circuit, analogous to the function of the emitter-follower with the transistor.


Figure 25
Figure 25
Modified Cathode Follower

The circuit variation of Figure 25 * provides a simple bias source for the cathode follower, and has added value because the input impedance is raised, an important factor in measuring equipment.

The resistor Rk1 is selected to furnish the proper bias, but shunted out of the equivalent circuit with the bypass capacitor. The AC output load is then Rk. Using the circuit relations:

Eg = E3 – Eo = RgIg

Eo = (Ig + gmEg) Rkrp/Rk + rp

The gain may be found by the equation:

Av = 1 / [1 + (Rg/1 + gmRk) (rp + Rk/rpRk)] (9-42)

and with gmRk>>1, the gain approaches unity.

The grid resistor Rg is connected between C1 and Rk in Figure 25, and the voltage at its cathode end is almost equal to and follows the voltage at the grid end. Since the voltage across Rg is Es in the cathode follower of Figure 24 *, and only Es – Eo in Figure 25, the current Ig is less in the latter case. The input resistance is found to be greater than Rg, as:

Rin = Es/Ig = Rg(1 + Eo/Es – Eo) = Rg(1/1 – A) (9-43)

The circuit can be designed to have a very high Rin value.



Composite Valve Amplifiers
Figure 26
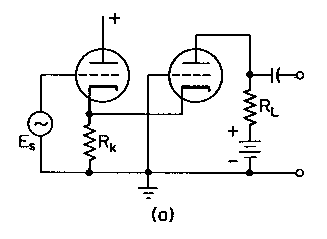
Figure 26

Cathode Coupled Circuit
The output impedance of a cathode follower is low. The input impedance of a grounded-grid amplifier is low. A cathode follower then is suitable for exciting a grounded-grid stage; the result provides the input impedance of the cathode follower and the gain of the grounded-grid amplifier. Such a two-valve circuit is said to be cathode-coupled, and a circuit is shown in Figure 26 *.

Ordinarily the two valves are identical triodes, and:

Es – Egl = RkI1 – RkI2

μ Eg1 = (rp + Rk)I1 – RkI2

–μ Ek = μ Eg2 = Rk(I1 – I2) – (rp + RL)I2\br \br It is then possible to write:

Ao = Eo/Es = μ RL / rp[2 + (rp + RL) / ((μ + 1)Rk)] + RL

The cathode-coupled amplifier behaves like a grounded-cathode stage having a valve of amplification factor μ and an anode resistance greater than twice rp of one of the triodes. Although maximum gain is theoretically obtained with Rk large, the value giving correct bias is usually satisfactory.


Figure 27
Figure 27

Cascode Circuit
A composite circuit consisting of a grounded-cathode triode followed by a grounded-grid triode is often adopted for high-frequency amplification, because of several desirable characteristics. It is called a cascode amplifier and appears in Figure 27 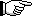*; often it uses a dual triode.

The load on the first triode is the input resistance of the grounded-grid triode as:

Ri2 = (rp2 + RL) / (μ 2 + 1)

and so the overall gain can be written as the product of the gains Av = Av1Av2, or

Av = (–μ 1Ri2/Rp1 + Ri2) [(μ 2 + 1)RL/rp2 + RL] (9-45)

For reasonably small values of RL it can be expected that

rp1 >> Ri2

and so

Av @ – gm1RL (9-46)

which is the gain of a pentode with transconductance gm1.

The gain of the grounded-cathode stage of the cascode amplifier is low because of the low load presented to it by the second valve, and so its input capacitance is not appreciably increased due to the Miller effect. Thus its input capacitance approximates Cgp, and at high frequencies its loading on the source is small. Because of the low value of Ri2, the input capacitance of the grounded-grid valve has small effect; therefore the circuit is a useful high-frequency amplifier.

While it would appear to be replaceable by a single pentode, the circuit is found to introduce much less circuit noise than does a pentode, and this is an important factor when working with very small input signals, such as RF amplifiers for radio receivers, for the same reason mentioned in the description for Common-Grid Amplifiers above.



Proceed to: [Valve Transformer Design]


*